Wordsworth Timing
Building on the discussion of basic Morse code timing and Farnsworth timing, we can explore the concept of Wordsworth timing. This approach also aims to enhance the recognition of Morse code, but it does so by keeping whole words at full speed and just increasing the gaps between them. It might be used by someone who had achieved instant character recognition but needed a little extra time to recognise and process each word. Whereas Farnsworth timing was named after Donald R. "Russ" Farnsworth (W6TTB), "Wordsworth" timing is (presumably) just a play on the word "Farnsworth" with a nod to the surname of the famous poet.
The chart below shows the concept. The sentence “PARIS PARIS PARIS PARIS ” is displayed at 20 wpm, and the toggle switch allows you to change to 15 wpm Wordsworth timing:
The “Wordsworth” toggle button shows how the timing changes when a 15 wpm Wordsworth speed is applied: changing the total length of “PARIS ” (including the final inter-word space) from 3000 ms to 4000 ms while leaving the timing of the individual characters in tact.
The speed of the words is determined by the normal WPM speed ($s_{wpm}$), and we define the Wordsworth speed ($s_{word}$) as well and use this to determine the actual number of words per minute. That is:
- Within each word:
- Dit: 1 unit (or $t_{dit}$)
- Dah: 3 units (or $3t_{dit}$)
- Intra-character space: 1 unit (or $t_{dit}$)
- Inter-character space: 3 units (or $3t_{dit}$)
- Between words:
- Word space: at least 7 Wordsworth-units (or $7t_{wdit}$)
where one Wordsworth-unit, $t_{wdit}$, is longer than the basic unit.
To keep the words at the $s_{wpm}$ speed, of the 50 dit units in “PARIS ” the part that we need to stretch out is the word space (7 units) and the part that needs to stay at the same speed is 43 standard $t_{dit}$ units within the words (the dits, dahs, intra-character and inter-character spaces).
The length of a dit is therefore the same as before:
$$ t_{dit} = {60 \over 50 s_{wpm}} \label{tdit} $$For the length of the word “PARIS ” we use the slower Farnsworth words per minute speed, or $s_{word}$. One word (“PARIS ”) should take this many seconds:
$$ \text{time to transmit `PARIS '} = {60 \over s_{word}} \text{ seconds} \label{paris} $$The time for the 43 standard units in “PARIS ” should be this many seconds:
$$ \text{time for the 43 standard units in `PARIS '} = 43 \times t_{dit} \text{ seconds} \label{paris43} $$Subtracting \eqref{paris43} from \eqref{paris} leaves the amount of seconds for the word space:
$$ \text{time for 7 Wordsworth units} = {60 \over s_{word}} - 43 t_{dit} \text{ seconds} \nonumber $$There are 7 Wordsworth units, so each one takes this many seconds:
$$ \text{time for 1 Wordsworth unit} = t_{wdit} = {(60 / s_{word}) - 43 t_{dit} \over 7} \text{ seconds} \label{twdit} $$Using \eqref{twdit} we can then look at the ratio of $t_{wdit} / t_{dit}$
\begin{align} {t_{wdit} \over t_{dit}} &= {(60 / s_{word}) - 43 t_{dit} \over 7 t_{dit}} \nonumber \\ &= {60 / s_{word} \over 7 t_{dit}} - {43 t_{dit} \over 7 t_{dit}} \nonumber \\ &= {60 \over 7 s_{word} t_{dit}} - {43 \over 7} \label{ratio} \end{align}Substituting \eqref{tdit} into \eqref{ratio}:
\begin{align} {t_{wdit} \over t_{dit}} &= {60 \times 50 s_{wpm} \over 7 s_{word} \times 60} - {43 \over 7} \nonumber \\ &= {50 \over 7}\cdot{s_{wpm} \over s_{word}} - {43 \over 7} \nonumber \\ &= {50s_{wpm} - 43s_{word} \over 7s_{word}} \label{ratio2} \end{align}It’s easy to check that if $s_{word} = s_{wpm}$ then, using \eqref{ratio2} we see $t_{wdit} / t_{dit} = 1$ which makes sense.
Alternatively, we can substitute \eqref{tdit} into \eqref{twdit} to get an expression for $t_{wdit}$ in terms of the two speeds:
\begin{align} t_{wdit} &= { {60 \over s_{word}} - 43 t_{dit} \over 7} \nonumber \\ &= { {60 \over s_{word}} - {43 \times {60 \over 50 s_{wpm}}} \over 7} \nonumber \\ &= {60 \times 50 s_{wpm} - 43 \times 60 s_{word} \over 7 \times 50 s_{wpm} s_{word}} \nonumber \\ &= {300 s_{wpm} - 258 s_{word} \over 35 s_{wpm} s_{word}} \text{ seconds}\label{twdit2} \end{align}We can check that if $s_{word} = s_{wpm}$ then \eqref{twdit2} works out the same as \eqref{tdit}.
By taking $7 \times t_{wdit}$ we can derive the length of an inter-word space, $t_{wspace}$, in seconds:
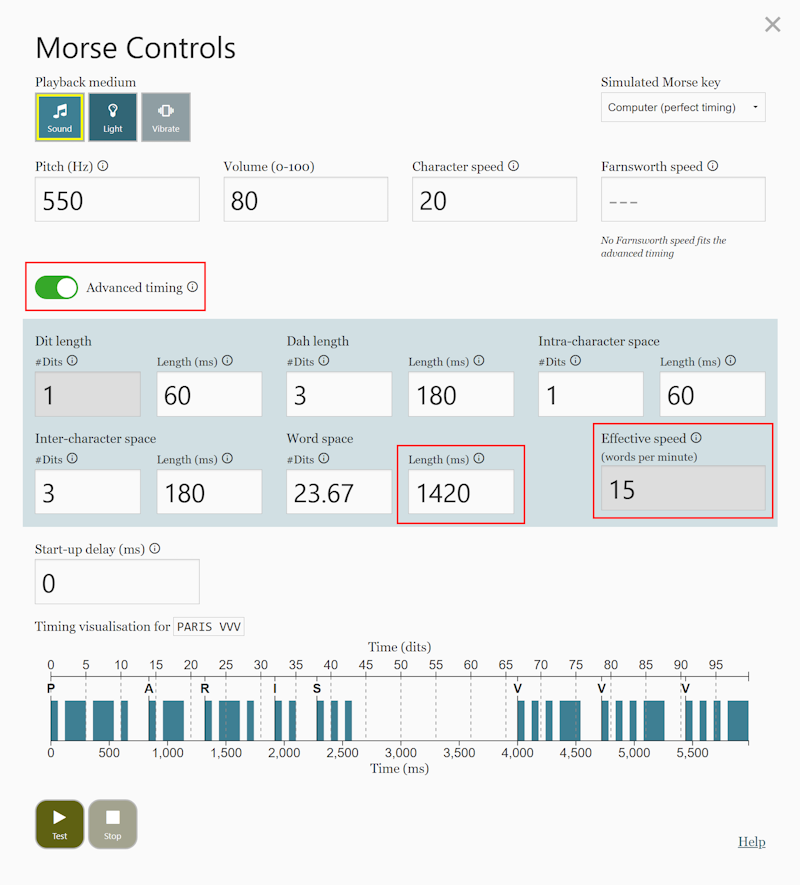
$$ t_{wspace} = 7 \times t_{wdit} = {300 s_{wpm} - 258 s_{word} \over 5 s_{wpm} s_{word}} \text{ seconds} $$The Morse Controls dialogue in the Morse Code World training tools does not directly support Wordsworth timing, but by opening the “Advanced timing” section, the word-space can be increased manually while keeping an eye on the “Effective Speed” value to achieve the effective words per minute required: